This article is for personal use to roughly review basic oriented bounding volume algorithms and practice JAX coding.
Caution
Before starting to read this article, I recommend you read the previous article about "Oriented Minimum Bounding Box" since it talks about the basic concepts of bounding volume and its need.
What is Bounding Volume?
According to the Wikipedia, we get a following definition about bounding volume.
In computer graphics and computational geometry, a bounding volume for a set of objects is a closed volume that completely contains the union of the objects in the set. Bounding volumes are used to improve the efficiency of geometrical operations by using simple volumes to contain more complex objects. Normally, simpler volumes have simpler ways to test for overlap.
Bounding volume is important for physics simulators in many aspects, such as ray tracing for rendering and collision detection for contact physics. Last time, I only talked about oriented bounding boxes, but there are many more geometric shapes that can be used. Normally, spheres, cylinders, and capsules are also used. Therefore, in this article, we will try the optimization method using differentiable computing to implement the bouding volume algorithm for different shapes.
1. Sphere
Bounding sphere algorithms are easier than others because the orientation does not matter in the sphere. Therefore, we usually call bounding sphere as miniball. Also, getting bounding sphere is simple and well-solved problem. Fisher's exact solver solves the problem less than the polynomial running time even in the worst case. There is even a direct python implementation of Fisher's solver. However, we will just try to implement an optimization method since our purpose is to practice JAX skills.
We optimize the Euclidean position of the center of the sphere because the radius is automatically decided for the bouncing sphere, which is the distance between the center and the furthest point from the center.
import jax
import jax.numpy as jnp
from jax import grad, jit
from jax.example_libraries import optimizers
@jit
def furthest_distance(t, mesh_vertices):
# t is an array of x,y,z coordinates of the sphere
return jnp.max(jnp.linalg.norm(mesh_vertices-t, axis=1))
@jit
def cost_function(mesh_vertices):
# mesh_vertices (nx3 array of mesh vertices)
def foo(t):
return furthest_distance(t,mesh vertices)
return foo
cost_f = cost_function(mesh_vertices)
derivative_fn = grad(cost_f)
# initialize the optimizer with the average position of the mesh vertices
initial_state = jnp.array(jnp.mean(mesh_vertices, axis=0))
opt_init, opt_update, get_params = optimizers.adam(step_size=1)
opt_state = opt_init(initial_state)
def learning_step(i, opt_state):
grads = derivative_fn(get_params(opt_state))
opt_state = opt_update(0, grads, opt_state)
return opt_state
@jit
def optimize():
return get_params(jax.lax.fori_loop(0, 100, learning_step, opt_state))
final_state = optimize()One simple trick for this algorithm is to set the initial value as the average position of points, which will reduce the converging time. Also, instead of using $\frac{4}{3}\pi r^3$ as the cost function, I used $r$, which converges stably because it is less affected by the size of $r$, which normally will not be zero.
The gradient of $\frac{4}{3}\pi r^3$ : $(\frac{4}{3}\pi r^3)'=4\pi r^2r'$
The gradient of $r$ : $(r)'=r'$

2. Cylinder
The bounding cylinder is usually used as a collision shape for people walking in the street to check the collision with the car. However, getting a bouding cylinder requires more complicated mathematics than the bouding sphere. Here we try to find the cylinder's center line. If we find the center line, the radius and height of the cylinder are automatically decided, using the line to point distance and point projection to the line. Let's say we have a 3D line, which is $\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$ where $\mathbf{x}_0=(x_0,y_0,z_0)$ and $d=(a,b,c)$. $d$ is a unit vector, meaning that its size is 1. Then, the distance between the line and the point $\mathbf{x}$ is
$$
|(\mathbf{x}-\mathbf{x}_0)\times(\mathbf{x}-\mathbf{x}_0-d)|$$
and the point projection to the line is
$$
(\mathbf{x}-\mathbf{x}_0)\cdot d$$
The radius of the cylinder is the maximum distance between the line and the points, and the height of the cylinder is the difference between the maximum and minimum projection of points onto the line. Therefore, we opimize $\mathbf{x}_0$ and $d$ with the cylinder volume as the cost function.
@jit
def cylinder_volume(xd, mesh_vertices):
# x: point in the line, d: inclination of the line
x, d = xd[:3], xd[3:]
# adjust the inclination if its size is 0
d = jnp.where(jnp.linalg.norm(d) != 0, d, jnp.array([1.,1.,1.]))
d /= jnp.linalg.norm(d) # change the inclination vector to unit vector
r = jnp.max(jnp.linalg.norm(jnp.cross(mesh_vertices-x, mesh_vertices-x-t), axis=1))
projected = jnp.inner(mesh_vertices-x, d) # project points to line
h = jnp.max(projected)-jnp.min(projected)
return r**2*h
@jit
def cost_function(mesh_vertices):
# mesh_vertices (nx3 array of mesh vertices)
def foo(xd):
return cylinder_volume(xd,mesh vertices)
return fooOne thing you have to be careful about is not making the inclination vector be a zero vector. I added a code to force the inclination vector to be (1,1,1) if that happens. For JAX code to be differentiable, you need to use a special code instead of using an if-statement.
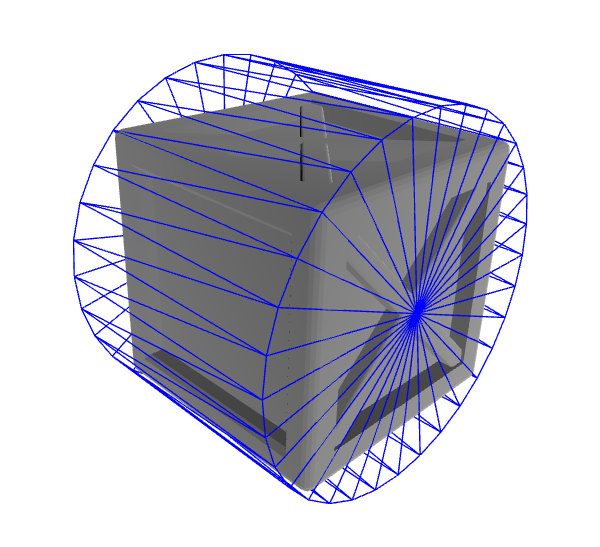
3. Capsule
Modern game engines more frequently use the capsule as a collision shape for humans. This is because it is easier to calculate the distance between a capsule and other shapes than a cylinder and other shapes. Also, you can create a fancier collision shape for humans by setting a capsul collision shape for each part of the human body, such as arms and legs. However, getting the bounding capsule is a bit more complicated than getting the cylinder. Here we try to find two Euclidean points. The radius of the capsule is automatically calculated when two points are decided, using the finite line to point distance. Let's say we have two points, $\mathbf{x}_1$ and $\mathbf{x}_2$. Then, the distance between the finite line and the point $\mathbf{x}$ is
$$
(p-a)-(b-a)t$$
where $t$ is
$$
clamp\left(\frac{(p-a)\cdot(b-a)}{(b-a)\cdot(b-a)},0,1\right)$$
The radius of the capsule is the maximum distance between the finite line and the points. Basically, if the projection of the point is out of two capsule points, the function calculates the distance between the point and the closest capsule point. And if the projection of the point is within the two capsule points, the function calculates the distance between the point and the line. Therefore, we optimize $\mathbf{x}_1$ and $\mathbf{x}_2$ with the capsule volume as the cost function.
@jit
def capsule_volume(xx, mesh_vertices):
# points of the capsule
a, b = x[:3], x[3:]
pb = mesh_vertices-a
ba = b - a
# check if a and b are the same points. If so, the capsule is a sphere
t = jnp.where(jnp.linalg.norm(ba) != 0,
jnp.clip(jnp.inner(pa,ba)/jnp.inner(ba,ba), 0.0, 1.0),
jnp.inner(pa,ba))
r = pa-jnp.repeat(jnp.expand_dims(ba, axis=0),t.shape[0], axis=0)*jnp.expand_dims(t, axis=1)
r = jnp.max(jnp.linalg.norm(r,axis=1))
h = jnp.linalg.norm(b - a)
return (h+4*r/3)*r**2
@jit
def cost_function(mesh_vertices):
# mesh_vertices (nx3 array of mesh vertices)
def foo(xx):
return capsule_volume(xx,mesh vertices)
return fooLike the sphere, you can initialize the value by the average of the points. Also, you have to be careful about the case where the two capsule points are the same because that's a sphere.

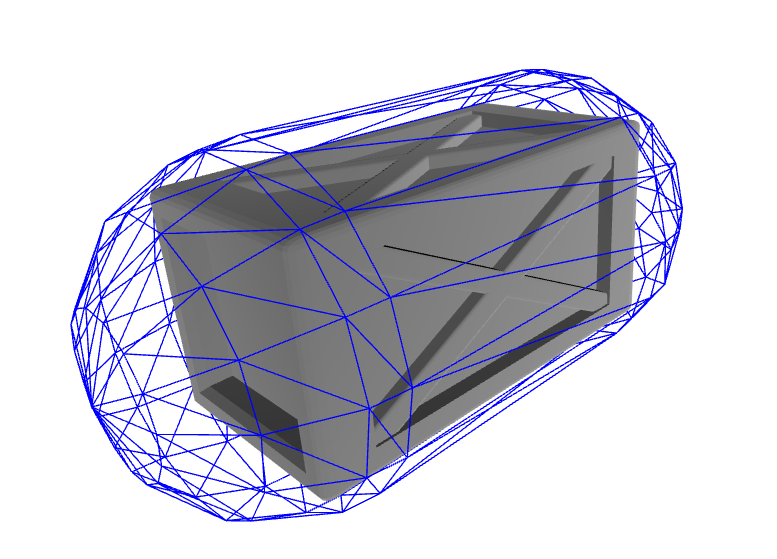
Elongated box:
'Physics Simulation' 카테고리의 다른 글
| Collision Detection - Dynamic AABB Tree (0) | 2023.01.08 |
|---|---|
| Mesh to Signed Distance Function (0) | 2022.11.21 |
| Signed Distance Function Visualization (0) | 2022.11.03 |
| Visualization of Physics Simulation in Google Colab (0) | 2022.10.08 |
| Oriented Minimum Bounding Box for 3D Mesh (1) | 2022.10.07 |