This article is for personal use to review and organize the existing way to visualize signed distance functions for 3D mesh using JAX.
What is Signed Distance Function (SDF)?
According to Wikipedia, we get the following definition about signed distance function.
In mathematics and its applications, the signed distance function (or oriented distance function) is the orthogonal distance of a given point x to the boundary of a set Ω in a metric space, with the sign determined by whether or not x is in the interior of Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω. However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside).

We follow the rule that the interior of Ω is negative, which is mostly used. Thus, the signed distance function of a circle with radius 1 will look like the image above where inner part of the circle have negative values. Signed distance functions are used to render 3D objects or calculate collisions between particles and the static environment. For example, the Unreal Engine, Unity, Blender, Godot, and many other game or graphic engines use SDFs to speed up shadow calculation and global illumination for realistic renderings of static objects. Also, many non-rigid object or particle simulations for clothing and liquids use SDFs. Our ultimate goal is to create SDFs for mesh and do collision detection, but visualization needs to be implemented first to find out if our created SDFs are without defects. Therefore, in this article, we look for a way to visualize simple geometric SDFs and grid SDFs, assuming that we already have grid SDFs for complicated mesh.
Sphere-assisted Ray marching
According to Wikipedia, we get the following definition about sphere-assisted ray marching.
In sphere tracing, or sphere-assisted ray marching an intersection point is approximated between the ray and a surface defined by a signed distance function (SDF). The SDF is evaluated for each iteration in order to be able take as large steps as possible without missing any part of the surface. A threshold is used to cancel further iteration when a point has reached that is close enough to the surface.
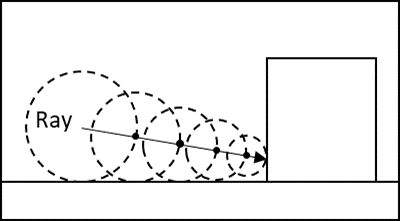
Many people who are interested in games or animation probably have heard about ray tracing technology, which enables the realistic rendering of 3D objects. Nvidia even sells GPUs that have special cores that are dedicated to ray tracing; they are called RTX GPUs. Ray marching is similar to ray tracing except that it uses SDFs to speed up the rendering by recursively marching the safe distance sphere to get the hit point, whereas ray tracing has to calculate the intersection or distance between a ray and all mesh triangles. It's a bit repetitive for me to explain this since it is very well documented and explained by Inigo Quilez. If you want to know more about ray marching, visit [his blog](https://iquilezles.org/).
Most of my codes are based on the tutorial shared by Alexander Mordvintsev from Google Research. He is a fascinating artist and a researcher and explains well how to implement ray marching using JAX. This article assumes that you have basic knowledge of ray marching. Therefore, if you do not want to get bombarded by new concepts in this article, please read his tutorial before we get into other things. The different things that I'll deal with here are ways to visualize geometric objects other than sphere shapes and grid SDFs.
Geometric SDF Visualization
Inigo Quilez explains many different kinds of SDFs for geometric shapes like box, cylinder, and so on. However, if you naively implement 3D geomtric SDFs from Inigo Quilez's blog, you will find glitches in your results mostly because of gradients of size zero.
Gradients of size zero
Rather than getting surface normals from the objects directly, Alexander Mordvintsev uses the gradient function of JAX to get normal data to render realistic shadows. However, he only renders sphere, which has no zero or near-zero gradients outside the object.
$$
Distance: \sqrt{(x-x_{sphere})^2+(y-y_{sphere})^2+(z-z_{sphere})^2}-r\\
Gradient: (2(x-x_{sphere}),2(y-y_{sphere}),2(z-z_{sphere}))$$
However, if you start to implement other shapes, you will find that normals you get are weird. This is because if you calculate the normals at ray hit poses, sometimes the size of gradients might come out as zero, especially if there is not enough curvature to the shape. Then, I recommend you first start looking at functions like clamp, min, and max functions since you can change those functions to make the distance function output a gradient to be a very small non-zero output even when it is actually zero. For example, the SDF for a box centered at origin and aligned with axes is like this:
def box_sdf(half_box_length, position):
d = jp.abs(position)-half_box_length
#s = jp.sign(position)
g = jp.max(d)
#gradient = s * jp.where(g>0.0, jp.clip(d,0,None)/jp.linalg.norm(jp.clip(d,0,None)),
# jp.heaviside(d[jp.array([1, 2, 0])],d)*jp.heaviside(d[jp.array([2, 0, 1])],d))
distance = jp.linalg.norm(jp.clip(d,0,None)) + jp.clip(g,None,0)
return distance#, normal
You can see that $d$ goes near to 0 when poistion gets near to the surface. Since normals are normalized gradients, if the gradient is near zero, things do not get calculated correctly by JAX gradient like in the surface normal from the middle of the above image. Now, based on the situation, if we use max or min function like below
$$
max(x,y)=\frac{x+y+\sqrt{(x-y)^2+\epsilon}}{2}\\
min(x,y)=\frac{x+y-\sqrt{(x-y)^2+\epsilon}}{2}$$
, we are able to get non-zero gradients. Those changed max and min functions are called smooth max and min functions. There are other ways to create smooth functions, but these are the simplest ones. And clamp function is just simple mixture of max and min function. For the case of box, where distance at the position is calculated using max function with $x=d$ and $y=0$ and min function with $x=g$ and $y=0$, we can change the functions as below to create non-zero gradient.
$$
max(d,0)=\frac{d+\sqrt{d^2+\epsilon}}{2}\\
min(g,0)=\frac{g-\sqrt{g^2+\epsilon}}{2}$$
After we change functions, we get the below image. We can see that the cube got smoothed out, but it looks good overall.

Or we can just get an analytic solution that gets normal directly from the object like image above. The funny thing about this is that you still have to use the smooth max function for a good outcome since analytic solutions also suffer from zero normal. However, only the gradient function changes, and the original distance function does not have to be changed, unlike when using the JAX gradient function. Also, there is another easy method for an analytic solution, which is to save previous non-zero normal information and use that as a normal for ray hit poses. This works amazingly well.

I prefer to get normals directly from objects, unlike how Alexander Mordvintsev does. It's not because his method is bad. Actually, many game engines take similar approaches to his approach by calculating gradients using several distance function results with infinitesimal displacements, which rarely suffer from zero gradient problem. However, for a person who does not deal with crazily moving fractals that are hard to get normals, analytically calculating the normals of geomtric shapes by hand seemed more reasonable than using gradient function since it is simple. Also, there is another reason, but I will explain it later in this article.
Grid SDF Visualization
Not all functions for different shapes can be easily obtained. For example, it is really hard for a human to get the SDF for the shape of an elephant (actually, there is a work that has the SDf of an elephant by using several SDFs). Therefore, what most programs do is change existing meshes to grids with the bounding volume and distance information and interpolate them to create smooth SDF. Especially, the Unreal Engine uses this well.

If you see the SDF image provided by Unreal, you can see a kind of bounding box around each object. This is because the image shows the number of rays marching steps, which usually increases when they get into the bounding box of the object. And space that is outside the bounding box is usually skipped using the intersection of the ray tracing.

They calculate distance by adding the distance from the point to the bounding box and the distance from the hit point on the bounding box to the object by parsing the grid ($|d_1|+|d_2|$). This usually works well for the visualization but gives artifacts. Also, they are prone to skip very thin parts of the object because the distance is large. You can see this in the image from Unreal. Therefore, this blog article takes the approach of calculating the gradient of SDF at the hit point and adding two vectors to get the distance ($|d_1+d_2|$). This is not an exact solution, but it removes many artifacts and more accurate than the naive one.

The left image is the SDF of the bounding box, the middle image is the SDF of a sphere using $|d_1|+|d_2|$, and the right image is the SDF of a sphere using $|d_1+d_2|$. You can see that the wobbling artifact got smaller in the right image compared to the middle.
However, it is not efficient to get the gradient for each step when ray marching. Therefore, rather than saving only distance information in the grid, I decided to save gradient information as well because it is important for me to have an accurate SDF for the physics engine when I deal with continuous collision detection. Also, in the simulation environment for robots, there are not many rigid objects, which are usually at most 30 objects. Thus, I thought that the increase in distance grid size (x4) was okay, since it is still smaller compared to the mesh data of objects. This is why I previously said I preferred to get normals directly from objects because I already had gradient information about them in the form of grid data. After that design decision, I was able to get the following results after some coding for the grid SDF.

The first row is the 4x4x4 grid, the second row is the 8x8x8 grid, and the third row is the 16x16x16 grid. Since the shape is simple, small grids like 8x8x8 worked okay, but if you look closely at the shadow on the object, you will be able to see some diamond artifacts.

There is a paper that used gradient information to do a first-order Taylor approximation of SDF rather than the zero-order Taylor approximation that we used. I also implemented it, but it seemed to have worse results than the zero-order Taylor approximation. The sphere looked like a devil's fruit like above, and the distance function was showing artifacts. If there is anyone who succeeds in this, please share your experiences with it.

Moving grid SDF is exactly the same as moving geometric SDF. You just transform the parsed point to the object's coordinates and calculate the distance. For the gradient, you have to transform it from object coordinates to world coordinates. The below code is a code to simply create a grid SDF of a sphere of radius 1 and visualize it using trilinear interpolation.
import jax
import jax.numpy as jp
from functools import partial
res = 8 # resolution of maximum length of the bounding box
bbox_length = jp.array([2,2,2]) # x_l, y_l, z_l: bounding box length
base_l = jp.max(bbox_length)/(res-1) # actual grid length
xyz_res = jp.ceil(bbox_length/base_l+1e-4) # resolution for each axes
x_res, y_res, z_res = xyz_res.at[0].get(), xyz_res.at[1].get(), xyz_res.at[2].get()
x_ = jp.linspace(-base_l*x_res/2, base_l*x_res/2, x_res.astype(int))
y_ = jp.linspace(-base_l*y_res/2, base_l*y_res/2, y_res.astype(int))
z_ = jp.linspace(-base_l*z_res/2, base_l*z_res/2, z_res.astype(int))
x, y, z = jp.meshgrid(x_, y_, z_, indexing='ij')
# object position in SE(3)=(SO(3),t)
R = rotation_matrix(jp.pi/2, 0, 0)
t = jp.array([1.0,0.0,0.0])
def sphere_sdf(p):
gradient = p*2
distance = jp.linalg.norm(p,axis=-1)-1
w = distance
# w = distance - jp.sum(p*gradient, axis=-1) # first-order Taylor
return jp.concatenate((gradient, jp.expand_dims(w, axis=-1)), axis=-1, dtype=jp.float16)
distance_grid = sphere_sdf(jp.stack((x,y,z), axis=-1))
# save distance grid data
data_dict = {"bbox_length": bbox_length, "base_length": base_l, "resolution": xyz_res, "distance_grid": distance_grid}
jp.save('sphere_sdf.npy', data_dict)def parsing(parse):
# transform parsed pos to grid-scaled pos
pos = parse*(xyz_res-1)/(base_l*xyz_res)+(xyz_res-1)/2
id = pos.astype(int)
xid = jp.take(id, 0, axis=-1)
yid = jp.take(id, 1, axis=-1)
zid = jp.take(id, 2, axis=-1)
# trilinear interpolation
v000 = distance_grid.at[xid,yid,zid].get()
v100 = distance_grid.at[xid+1,yid,zid].get()
v010 = distance_grid.at[xid,yid+1,zid].get()
v001 = distance_grid.at[xid,yid,zid+1].get()
v101 = distance_grid.at[xid+1,yid,zid+1].get()
v011 = distance_grid.at[xid,yid+1,zid+1].get()
v110 = distance_grid.at[xid+1,yid+1,zid].get()
v111 = distance_grid.at[xid+1,yid+1,zid+1].get()
pos -= id
xp = jp.take(pos, 0, axis=-1)
yp = jp.take(pos, 1, axis=-1)
zp = jp.take(pos, 2, axis=-1)
d = v000*jp.expand_dims((1-xp)*(1-yp)*(1-zp), axis=-1) +\
v100*jp.expand_dims(xp*(1-yp)*(1-zp), axis=-1) +\
v010*jp.expand_dims((1-xp)*yp*(1-zp), axis=-1) +\
v001*jp.expand_dims((1-xp)*(1-yp)*zp, axis=-1) +\
v101*jp.expand_dims(xp*(1-yp)*zp, axis=-1) +\
v011*jp.expand_dims((1-xp)*yp*zp, axis=-1) +\
v110*jp.expand_dims(xp*yp*(1-zp), axis=-1) +\
v111*jp.expand_dims(xp*yp*zp, axis=-1)
parsed_grad = jp.take(d, jp.array([0,1,2]),axis=-1)
parsed_distance = jp.take(d, 3, axis=-1)
# parsed_distance = jp.sum(parsed_grad*parse, axis=-1) + jp.take(d, 3, axis=-1) # first-order Taylor
return parsed_distance, parsed_grad# calculate distance inside bounding box
def in_sdf(p,d,s,g):
return parsing(p)
# calculate distance outside bounding box
def out_sdf(p,d,s,g):
box_normal = s * jp.clip(d,0,None)/jp.linalg.norm(jp.clip(d,0,None))
box_distance= jp.linalg.norm(jp.clip(d,0,None)) + jp.clip(g,None,0)
hit_pos = p-box_distance*box_normal
object_distance, object_normal = parsing(hit_pos)
distance = jp.linalg.norm(length*box_normal + sphere_length*sphere_normal/norm(sphere_normal))
# distance = box_distance + object_distance # Unreal engine's method
return distance, sphere_normal
@jax.jit
def object_sdf(rad, p):
# world coordinate to object coordinate transformation
p_transform = jp.linalg.inv(R)@p-jp.linalg.inv(R)@t
d = jp.abs(p_transform)-rad
s = jp.sign(p_transform)
g = jp.max(d)
distance, object_norm = jax.lax.cond(g<0.0,in_sdf,out_sdf,p_transform,d,s,g)
# object coordinate to world coordinate transformation
object_norm = R@object_norm
return distance, object_normdef raycast(sdf, p0, dir, step_n=100):
def f(_, pn):
p_prev, n_prev = pn
p_new, n_new = sdf(p_prev)
# return ray-marched position and non-zero gradeint
return (p_prev+p_new*dir, jp.where(jp.linalg.norm(n_new)>0, n_new, n_prev))
return jax.lax.fori_loop(0, step_n, f, (p0, p0))
world_up = jp.array([0., 1., 0.])
def camera_rays(forward, view_size, fx=0.6):
right = jp.cross(forward, world_up)
down = jp.cross(right, forward)
R = normalize(jp.vstack([right, down, forward]))
w, h = view_size
fy = fx/w*h
y, x = jp.mgrid[fy:-fy:h*1j, -fx:fx:w*1j].reshape(2, -1)
return normalize(jp.c_[x, y, jp.ones_like(x)]) @ R
w, h = 640, 400 # image size
pos0 = jp.float32([3.0, 5.0, 4.0]) # camera pos
ray_dir = camera_rays(-pos0, view_size=(w, h))
sdf = partial(scene_sdf, jp.array([1,1,1]))
hit_pos, raw_normal = jax.vmap(partial(raycast, sdf, pos0))(ray_dir)
imshow(hit_pos.reshape(h, w, 3)%1.0)
imshow(raw_normal.reshape(h, w, 3))The way to convert mesh to SDF will be discussed in a future article. It will be based mainly on the previous blog article I mentioned briefly since it can be modified to get gradient information easily. However, I will also mention about other methods, which is less accurate but faster.
'Physics Simulation' 카테고리의 다른 글
| Collision Detection - Dynamic AABB Tree (0) | 2023.01.08 |
|---|---|
| Mesh to Signed Distance Function (0) | 2022.11.21 |
| Oriented Minimum Bounding Volume for 3D Mesh (0) | 2022.10.19 |
| Visualization of Physics Simulation in Google Colab (0) | 2022.10.08 |
| Oriented Minimum Bounding Box for 3D Mesh (1) | 2022.10.07 |